Prime Numbers, the Extended Euclidean Algorithm, and the GCD¶
This is the second post in a short series on the RSA algorithm. The first post was an overview of modular arithmetic, and this article will attempt to cover a few more ideas needed before we dig into the weeds of the algorithm. It may seem like I am jumping around a bit, but I think this highlights the brilliance of Rivest, Shamir, and Adleman. They were able to compose an algorithm from pieces that may not seem immediately related to one another.
A note on studying¶
I skipped some important points in the last article hoping to spark a few people's interest. I will continue with the goal of keeping the writing light, but we do have to work with a few important theorems and definitions along the way. Some of the best math advice I ever heard or read is that whenever you are faced with a Definition or a Theorem, stop what you are doing and write down some examples! "The Math Sorcerer" has a great video about self-study on YouTube.
More review¶
Formally speaking, the Division Algorithm is the basis of modular arithmetic. This may feel pedantic, but the aim is to build our argument in small, clear steps.
Definition: Division Algorithm¶
For all integers $a$ and $m$ with $m>0$, there exist unique integers $q$ and $r$ such that $$a=mq+r$$ where $0≤r<m$ (Cummings 2022).
A bar or "pipe" is used to mean divides. For example, if you see $3|6$, this means that 3 divides 6. A bar with a slash across it means doesn't divide. $3\nmid 7$. One integer divides another only if the remainder is zero.
Theorem: Modular arithmetic¶
For integers $a$,$r$, and $m$, it is said that $a$ is congruent to $r$ modulo $m$, and one writes $a \equiv r \pmod m$, if $m|(a−r)$ (Cummings 2022).
This concept should be familiar if you read my last article. The new piece here is the idea of congruency.
Equivalent, but not equal¶
You will see the word "congruent" in almost any article about the mathematical machinery of the RSA algorithm. We all know that 4 is not equal to 16. But what about our $\pmod{12}$ number system? We can exchange them in equations and get the same result. This is what it means to be congruent. In a modular system, we say that 4 is congruent to 16 in $\pmod{12}$. This is a good point to stop and write down some examples of your own!
Prime numbers¶
I hope you aren't bored yet! Number theory begins with many of the ideas you were taught about whole numbers as a child. Prime numbers play a key role in RSA. What does it mean to be prime? Prime numbers are the "atoms" of the integers; they compose all other integers. I have a bag of small wooden cubes that I have used when teaching my kids math. A prime number is a number that can only be arranged in a line. Composite numbers can be built as rectangles, squares or 3-dimensional combinations of squares and rectangles.
Homework¶
I leave prime factorization and a formal definition of primes as an exercise for the reader.
If you are a programmer, write an implementation of the Sieve of Eratosthenes in your favorite language.
Want an old-school challenge?
Write it in awk.
GCD¶
Theorem: Greatest common divisor¶
Let $a$ and $b$ be integers. If $c|a$ and $c|b$ ,then $c$ is said to be a common divisor of $a$ and $b$. The greatest common divisor of $a$ and $b$ is the largest integer $d$ such that $d|a$ and $d|b$. This number is denoted $gcd(a,b)$ (Cummings 2022).
This should be more grade school maths.
- $\gcd(20, 24) = 4$
- $\gcd(28, 35) = 7$
Co-prime numbers¶
Two numbers are called "co-prime" if they only have 1 as a common divisor. In other words, their GCD = 1. Some examples of co-prime pairs:
- 7, 13
- 24, 71
- 112341234120042, 112341234120043
Take a look at that last one and notice that they differ by 1. Take a moment and convince yourself that any two integers with a difference of 1 are co-prime. Are you convinced?
Homework¶
Use this fact to explore one of the earliest proofs that there are an infinite number of primes!
Euler's totient function¶

This guy shows up everywhere in math, doesn't he?!
Euler's totient function is also known as the Euler $\phi$-function. Don't let the names spook you away; the concept is straightforward.
We are interested in how many numbers are co-prime with a number. This calls for examples. Think of the function as the length of a list.
- $\phi(7) = 6$ because 1, 2, 3, 4, 5, 6 are co-prime with 7; $\gcd(7, 1..6) = 1$.
$\phi$ of any prime number is equal to $p - 1$ by the definition of a prime number (you looked that up, earlier, right?).
- $\phi(11) = 10$
- $\phi(65537) = 65536$, AKA $(2^{16} + 1)$ and $2^{16}$ for you programmers.
Composite numbers are a little trickier. We have to perform a prime factorization and eliminate numbers with any common factors $\ne$ 1 (because 1 is a divisor of all integers).
- $\phi(24) = 8$ because 1, 5, 7, 11, 13, 17, 19, 23 are co-prime with 24.
Again, 8 is the length of this list.
This topic will be new to many of you without much college-level math, even former engineering students. It is not horribly complicated at first sight, but my brain exploded when I saw it used in other formulas... Spoiler alert, we will see it used in another formula!
Prime factorization¶
The strength of RSA depends solely on the ability to factor large numbers. Quantum computers could theoretically provide a huge increase in our ability to factor these numbers, and efforts are underway by governments, academic institutions, and corporations to find replacement algorithms that are "post-quantum" safe. If you want to know more about this, do a search for Peter Shor's algorithm. The NIST (USA) has already chosen one key exchange suite called Kyber. As of this writing, it has not been standardized, but companies such as Google and Cloudflare are fast at work deploying it across their networks (articles linked in their names). We don't have scalable quantum computers today, but there is a real threat that encrypted conversations recorded on the internet now could be decrypted in a decade or two.
Bézout's identity¶

We need one more theorem before I wrap up with the Euclidean algorithm. This theorem is very important to the inner machinery of RSA, so make sure you play with it and understand how it works.
Theorem: Bézout's identity¶
If $a$ and $b$ are positive integers, then there exist integers $k$ and $l$ such that $\gcd(a,b) =ak+bl$ (Cummings 2022).
Note that $k$ and $l$ aren't necessarily positive. Given $\gcd(28, 35) = 7$, how do we find $k$ and $l$? In this case, simple inspection tells us that $k=-1$ and $l=1$, thus
$$\gcd(28, 35)=(-1)(28) + (1)(35) = 7$$Do you think $k$ and $l$ are unique? Existence and uniqueness questions appear frequently in the study of mathematics.
7 and 3 are prime, and $\gcd(7, 3) = 1$.
$$\gcd(7, 3) = 1 = (-2)(3) + (1)(7)$$Before going much further, I want to introduce Cayley tables.
Cayley tables¶
Recall addition and multiplication tables from grade school. We can do the same thing in modular arithmetic systems. Using the $\pmod{3}$ system, here is the addition table:
| -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
+----+----+----+----+----+----+----+----+----+----+----+----+----+
-7 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
-6 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
-5 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
-4 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
-3 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
-2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
-1 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
0 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
1 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
2 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
3 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
4 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
And here is the multiplication table:
| -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
+----+----+----+----+----+----+----+----+----+----+----+----+----+
-7 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 |
-6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
-5 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
-4 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 |
-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
-2 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
-1 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 |
3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
These can be quite useful in your study of the modular world, and they will make another appearance in the next aritcle.
Back to Bézout¶
Do you notice any patterns in the previous tables? It may not be immediately obvious that the tables are helpful, so I will provide an additional clue. Consider a "clock" in $\pmod{3}$.
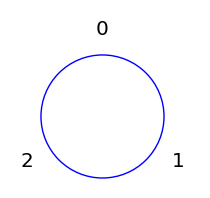
Now take a tape with all the integers (positive and negative) written on it. Center is at zero and wrap it around both ways. Write this down on a piece of paper; do you see the result? Pay special attention to where multiples of 7 land on the $\pmod{3}$ circle.
Again, Bézout tells us that there is a $k$ and $l$ that satisfies $\gcd(7, 3) =7k+3l$. Multiples of 7 give us $k$, and corresponding multiple of 3 give us $l$. I say corresponding because not every muliple of 3 will do. Notice that it takes two "wraps" of our tape to hit a multiple of 7.

Consider the sequence of differences between multiples of 7 and its nearest neighbor. This results in the sequence
$$[9−7, 15−14, 21−21, 30−28, 36−35, 42−42, 51−59, 57−56, . . .]$$or
$$[2, 1, 0, 2, 1, 0, 2, 1, . . .]$$The pattern should be clear, and one knows it repeats because of the properties of modular arithmetic.
I hope this is starting to make a bit of sense now. The symmetry of modular systems is fascinating to me, and I hope you have a better intuition of Bézout's identity. This is a critical Theorem, and I feel like it gets overlooked in a lot of math books and articles.
Extended Euclidean Algorithm¶
I am not going to spend much time on this point because the method well-documented in books and across the web. The mechanics of it should start to feel familiar by this point. If not, create some examples of your own and work a couple problems (you should do it regardless!).
The table here follows the procedure described by Brian Kell.
Beginning with $a=93060$ and $b=307$, use the division algorithm to find the values $q$ and $r$. $a$ and $b$ were chosen such that $\gcd(a,b) =1$. Back-substitute $a$ and $b$ appropriately, and iterate until the remainder is zero.
| c | d | q | r | out |
| 93060 | 307 | 303 | 39 | 39 = 93060 - (303)(307) = a - 303b |
| 307 | 39 | 7 | 34 | 34= 307 - 397 = b - 7(a - 303b) = -7a + 2122b |
| 39 | 34 | 1 | 5 | 5 = 39 - 34 = (a - 303b) - (-7a + 2122b) = 8a - 2425b |
| 34 | 5 | 6 | 4 | 4 = 34 - 65 = (-7a + 2122b) - 6(8a - 2425b) |
| 5 | 4 | 1 | 1 | 1 = 5 - 4 = (8a - 2425b) - (-55a + 161672b) = 63a - 19097b |
The last row gives us the values of $k$ and $l$ that can be plugged into Bézout's identity.
$$\gcd(93060, 307) = 1 = 63(93060) + -19097(307)$$Wrapping up¶
This article is quite a bit different than the last one, but we have to face the nitty-gritty details at some point. I hope you are starting to see the connections between these three subjects even though you may be wondering where all this is going. The next article will introduce the star of the show, the modular inverse! Don't worry, there will be no surprises there if you can understand the ideas in this post.
Resources¶
The web is full of great articles, but I stare at a screen all day. If you are interested in basic number theory and an absolutely incredible introduction to proofs, I highly recommend "Proofs: A Long-Form Mathematics Textbook" by Jay Cummings. For my technology friends, Kenneth Rosen's "Discrete mathematics and its applications" has earned itself a permanent spot on my desk. It covers the number theory used here as well as many other topics relevant to programmers.
References¶
- Cummings, J. (2021). Proofs: A Long-Form Mathematics Textbook.
- Judson, T. (2021). Abstract algebra: Theory and Applications. Orthogonal Publishing L3c.
- Kell, B. (2010). The extended euclidean algorithm. https://www.math.cmu.edu/~bkell/21110-2010s/extended-euclidean.html
- Rosen, K. (2011). Discrete mathematics and its applications. McGraw-Hill Education.
Photos¶
- Euler portrait: https://commons.wikimedia.org/wiki/File:Leonhard_Euler_2.jpg
- Bézout portrait: https://mathshistory.st-andrews.ac.uk/Biographies/Bezout/